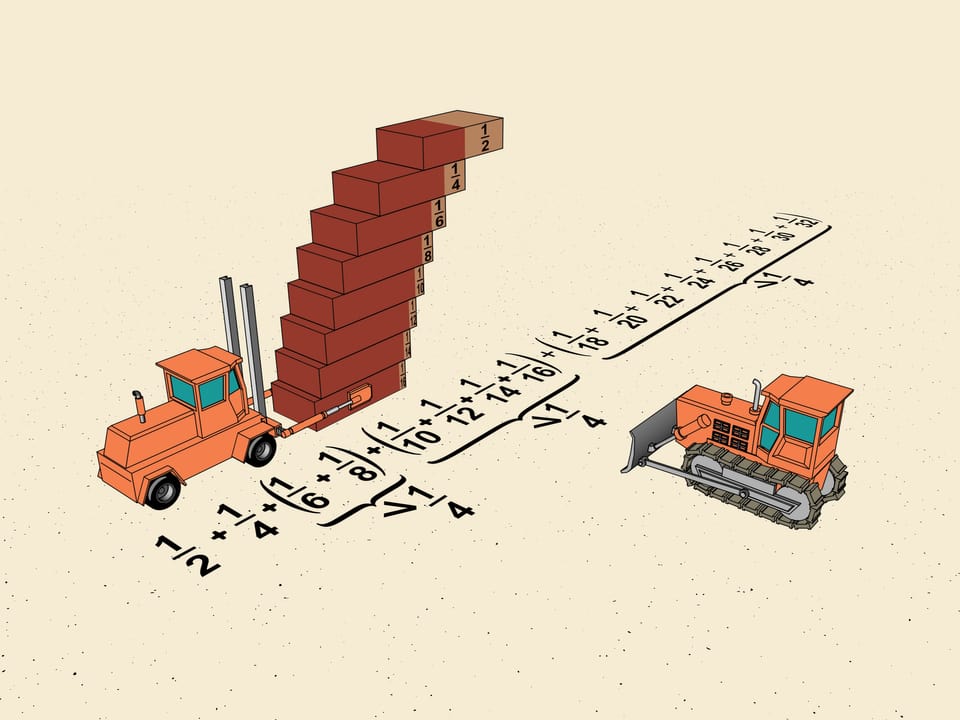
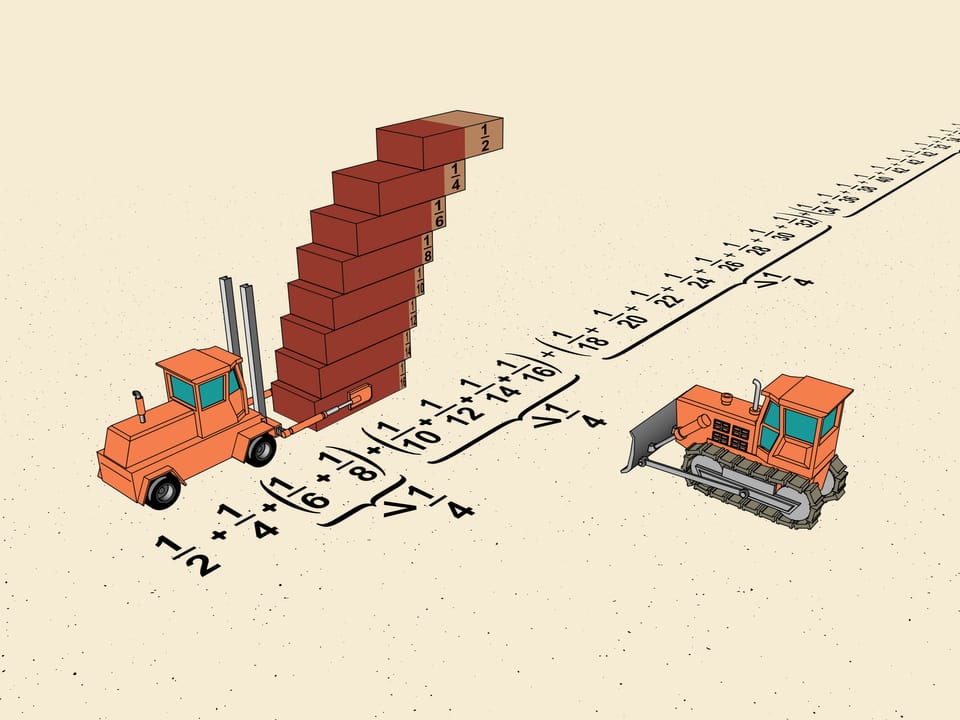
Where should one take a brick so that it stays balanced? Certainly in the center. The center of gravity of a single brick is on the central line. Thus, one may place this brick on another, shifting half of its length with respect to the lower, and it won't fall.
And where should one of the brick length. Indeed, the center of gravity of the upper brick projects on the border of the lower, the same mass is placed in the center of the lower brick. Thus, the center of gravity of the system is in the middle of a half of a brick, i.e. $1/4$ length away from the edge.
A tractor length away from its edge.
A butterfly is a light creature, the loader is pleased to play with it. But look, it lands on the bricks. If it lands on a point that more to the right and the ladder starts falling apart. The loader has to speed up to keep the construction stable. This shows again that the shifts $1/2$ and $1/4$ of the brick length are the maximal when the construction is stable without cement.
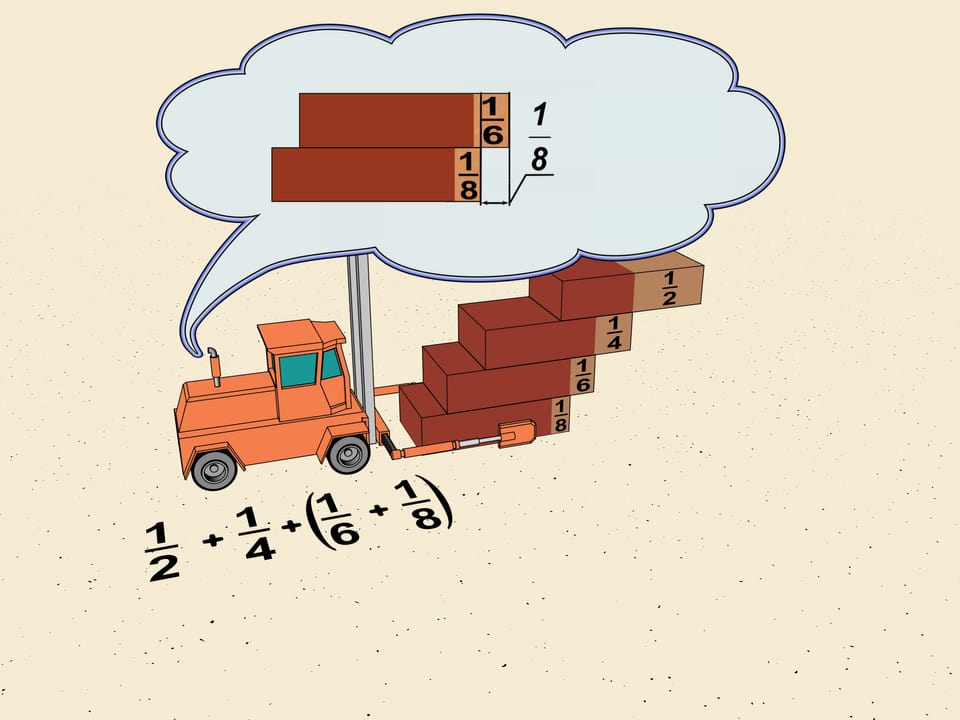
And where is the center of gravity of the three-brick system? The center of gravity of the upper two projects on the edge of the lower one. The center of gravity of the latter is in the middle. But now the masses are different: to the right we have a mass of two bricks and to the left of a single one. Thus the line containing the center of gravity of the system with chosen shifts divides a half of the brick as $2:1$, counting from the center. I.e. passes $ 1/6$ brick length from the edge.
We can use this method to calculate that without using cement one can build a ladder moving n upper bricks $1/2n$ brick length from the edge of the lower. We'll continue doing this obtaining the maximal horizontal shift.
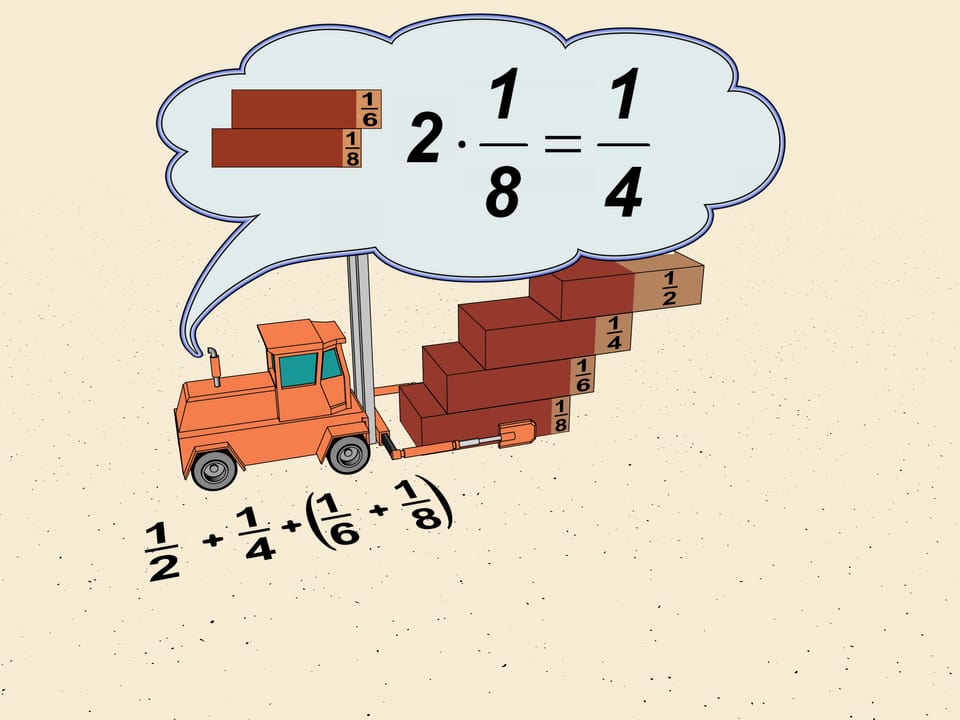
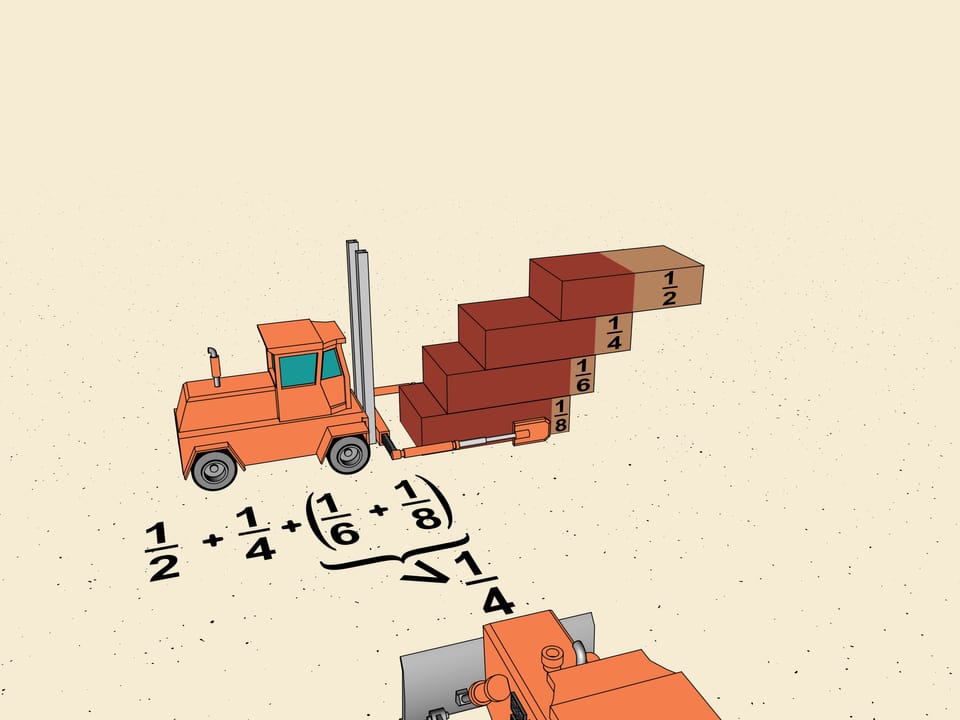
Consider the first shifts of our ladder. It's $1/2, 1/4, 1/6, 1/8$. Without touching the first two group $ 1/6$ and $1/8$, as mathematicians say, in a "block". Shift the upper brick so that the shifts in the block are equal to the minimal which is $1/8$. The total shift will be $2\cdot1/8=1/4$. We get that the horizontal shift given by this block is greater (we reshifted one brick) that $1/4$ of the brick length.
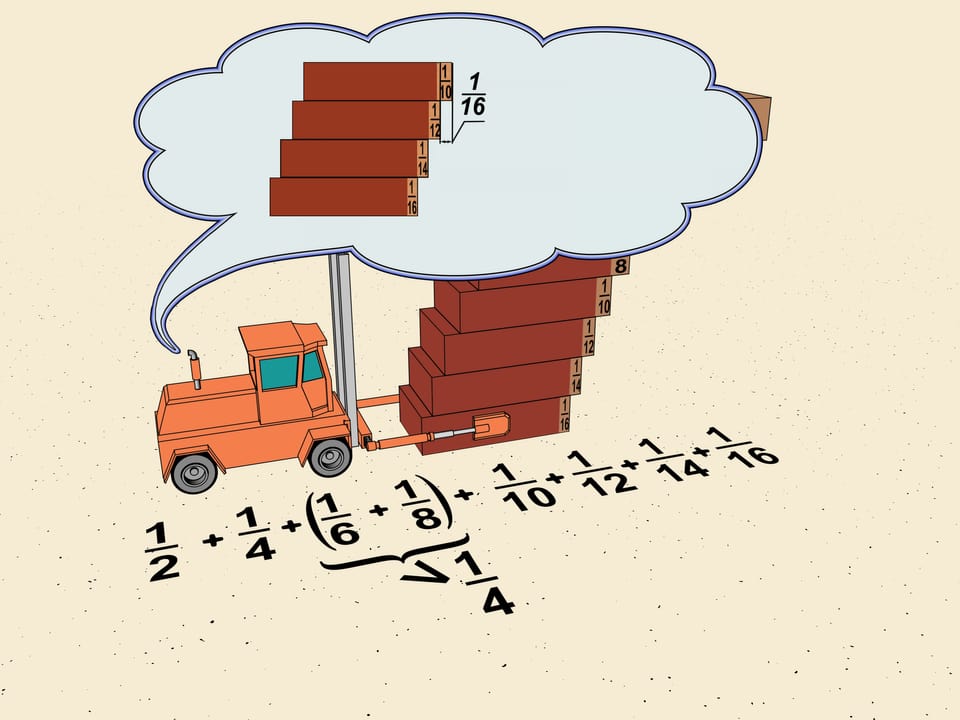
We choose how to divide our ladder into blocks. The next block we consider will of the brick length. You see the general scheme? The next block will consist of $2^{3}$ bricks and the minimal shift will be $1/2^{5}$ of the brick length. So, the total shift given by this block will be also greater than $1/4=2^{3}\cdot1/2^{5}$.
The same procedure allows to divide our ladder into blocks. The block number n will contain $2^{n}$ bricks and the smallest shift in it will be $1/2^{n+2}$ of the brick length. The total shift of the block will be greater than $2^n \cdot 1/2^{n+2} = 1/4$.
Multiply every member of the series by $2$ and reduce the fractions. We get the series $1+1/2+1/3+1/4+1/5+1/6+1/7+...+1/n+...$ This series is called harmonic series. It plays an important role and is in some sense boundary. If you build a ladder (using cement) with shifts greater than 1/n (i.e. the denominator will be less than n), it will go to infinity.
In mathematics such a property is called divergence: for any given number we may take sufficiently many first members so that its sum will be greater. One of the criteria of divergence is comparison with the harmonic series.
Leaving, the cars talk:
– Incredible, the ladder will be above this place too?
– Yes, we've shown that we can take any number of blocks, each of them longer than $1/4$ of the brick length...