Living on the Earth surface people thought for a long time that it was flat. We had to build some theories to guess that the Earth looks more like a ball. And only in the second part of the XX century we could look at our planet from the space and certify it visually.
The same happens in mathematics: considering the ambient space we can often learn more about some object.
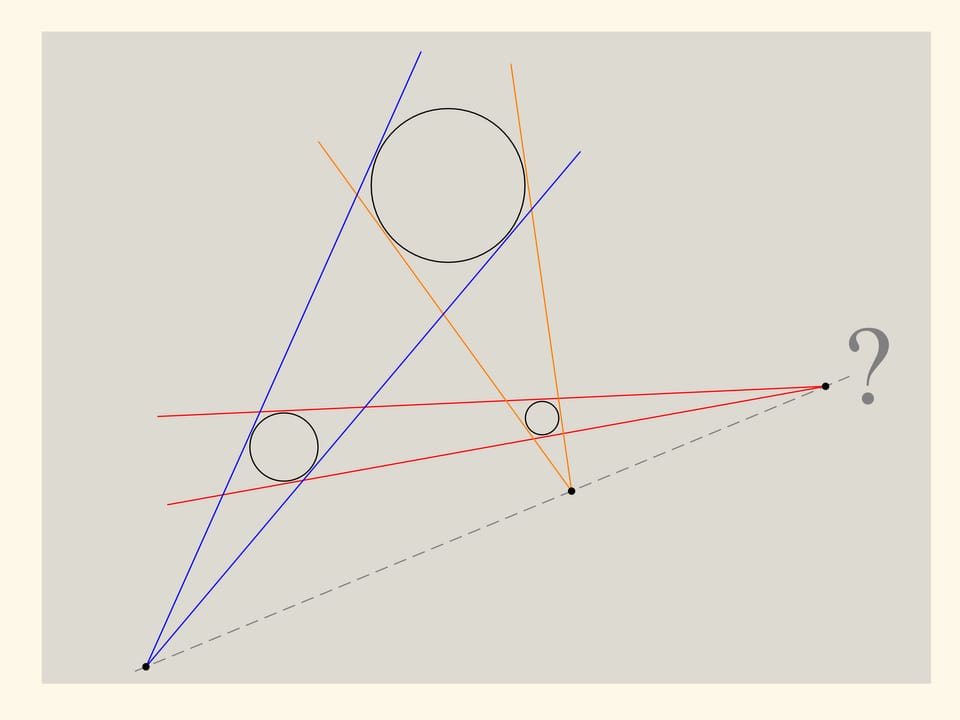
Consider three arbitrary circles and draw common tangents to every pair. What can we say about the single line. Well, a picture is not a proof, it's just a source for our conjecture. Let's try to prove it.
Both the problem and the image consider plane objects. But what if we look at them from outside, from the ambient three-dimensional space.
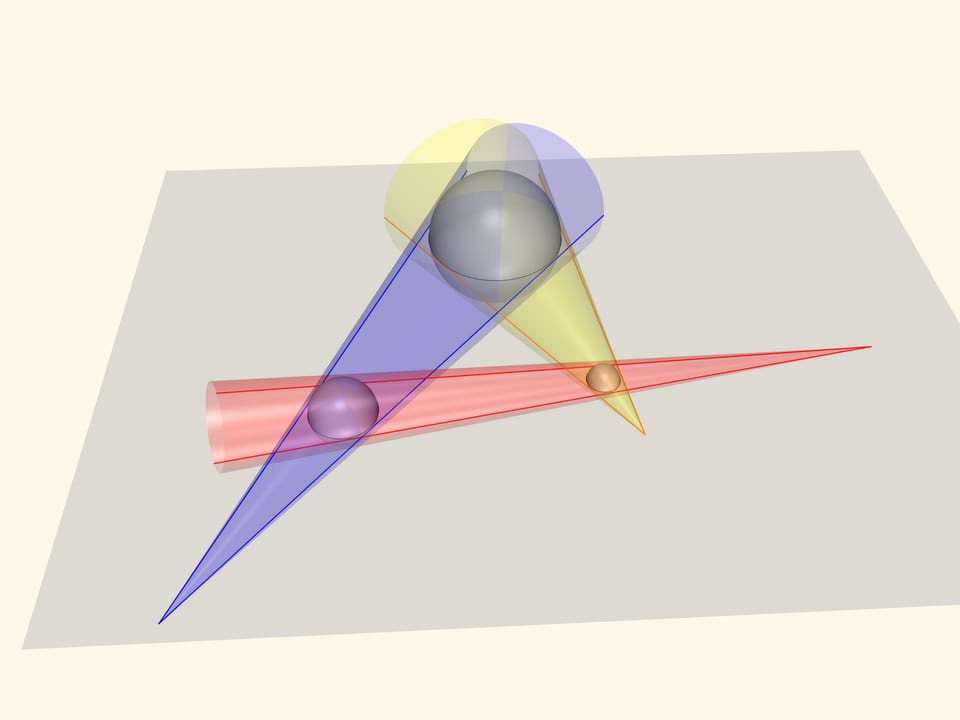
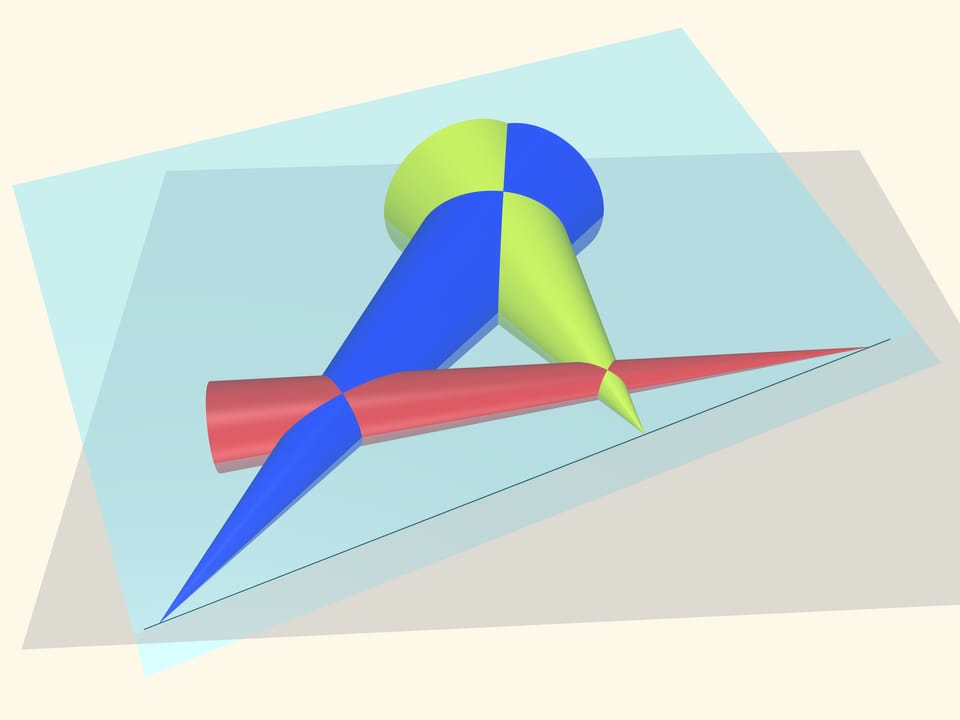
Consider three spheres whose equators are the circles. The cones enveloping the pairs of spheres have the common tangents as generatrices. The points we expect to lie on the same line are the apices of the cones.
Put a plane on the cones. The upper generatrices intersect pairwise and define this plane unambiguously. The points we a interested in, the cones apices, lie both on this plane and the «equatorial» one. But this two nonparallel planes have intersect in a line! So, as we conjectured, the three points of intersection of common tangents to three arbitrary circles lie on a single line.
Nowadays this theorem we've just proved is named after a french mathematician Gasrpard Monge.