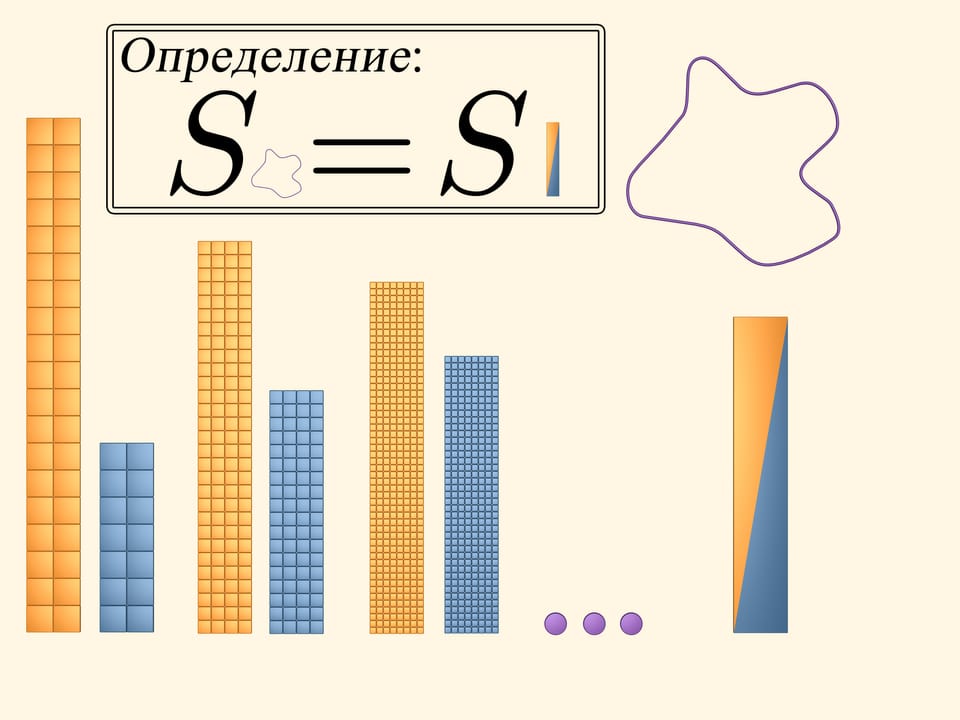
The area of a square equals to the square of it's side length. It's easy to compute the area of a figure that is built of several squares. And what is the area of a figure bounded by an arbitrary curve?
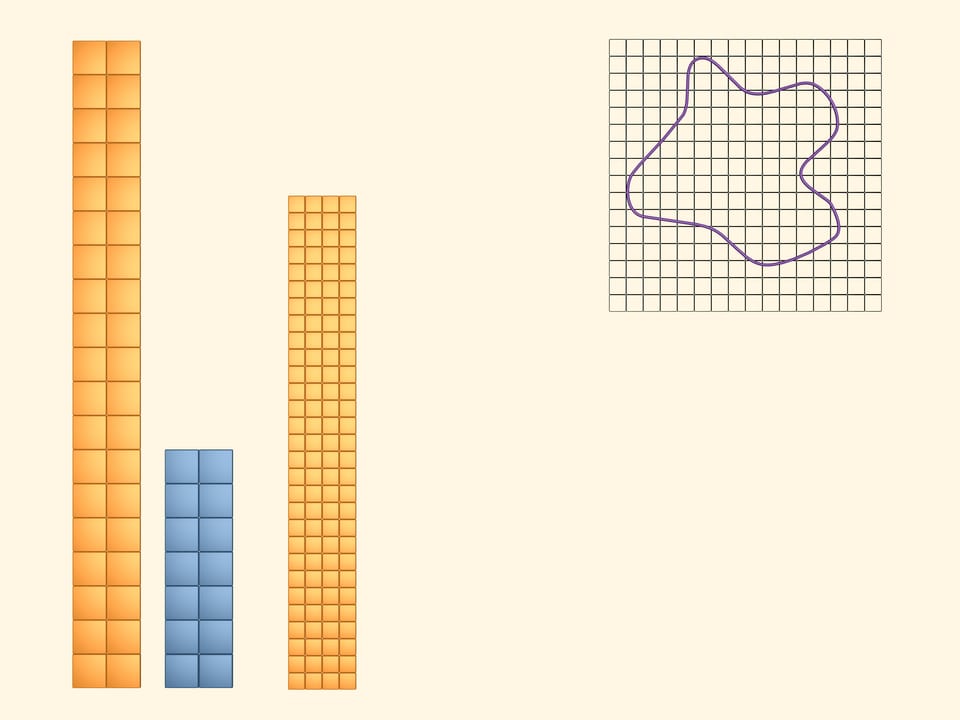
Place a square grid upon the measuring figure.
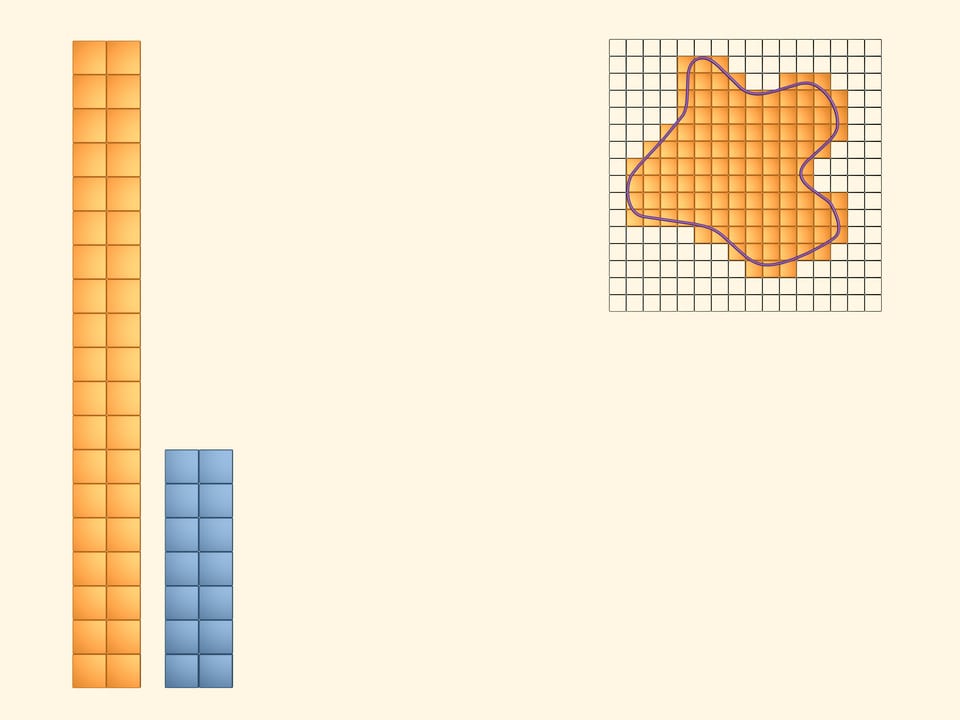
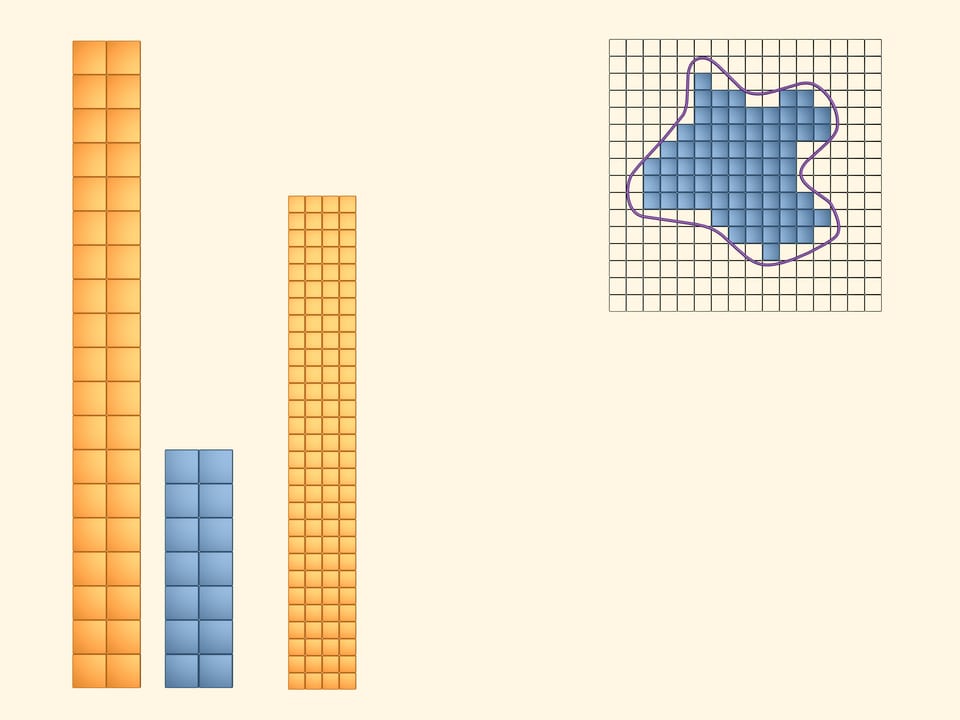
Paint in yellow the squares that even partially intersect the figure. To see and compute the area they cover, arrange them into a rectangle. It's obvious that the area of the studied figure is less than the area of the yellow rectangle.
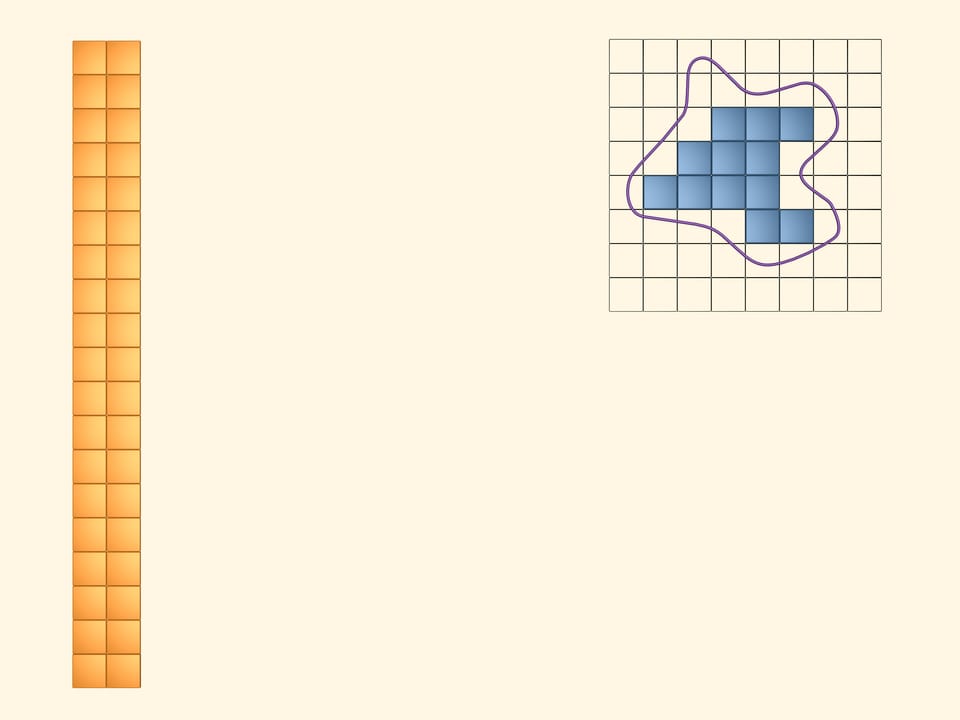
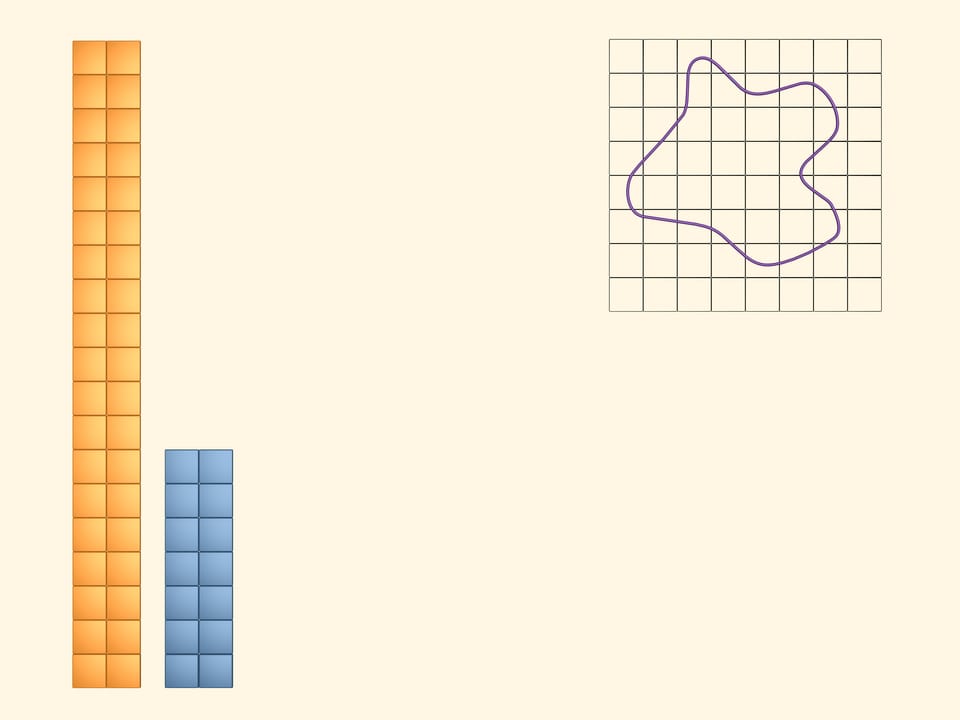
Next, paint in blue those squares that lie completely inside. Of course, there is less of them than the yellow ones. Put them together into a rectangle. The area of our figure is greater than the area of the blue rectangle.
Thus, whatever the area of our figure is, it's greater than the area of the blue rectangle and less than the area of the yellow one. But the bounds differ much and, for the moment, we can't imagine precisely the area we are computing.
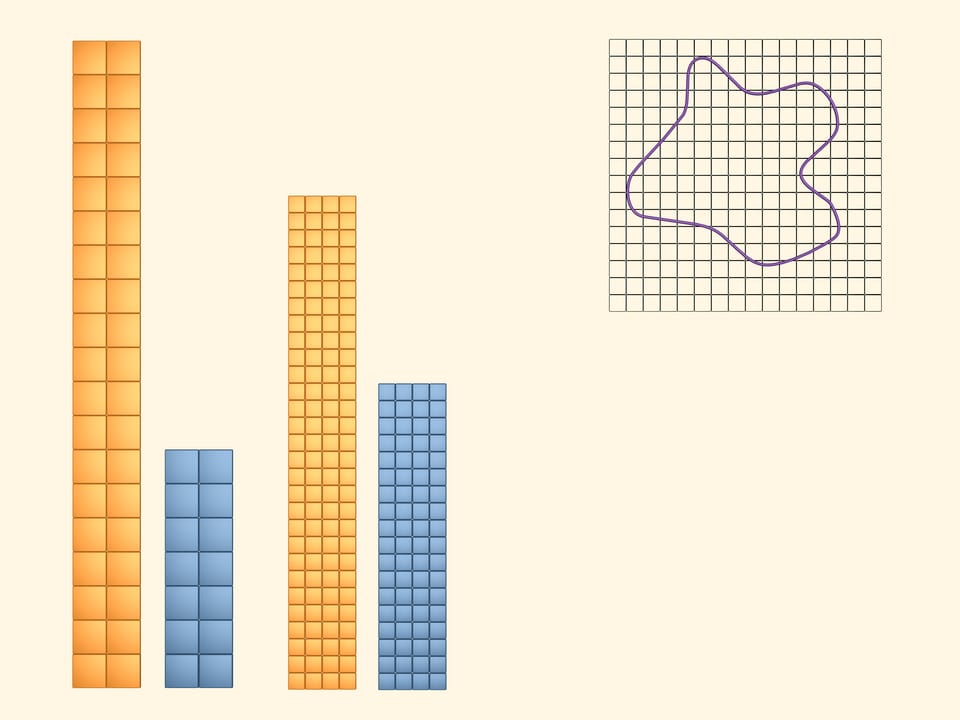
To get more precise upper and lower bounds, consider a partially intersect the figure and in blue those that lie completely inside. The area of the figure is again greater than the area of the blue rectangle and less than the area of the yellow one. But as we took a more frequent net, we got more precise bounds.
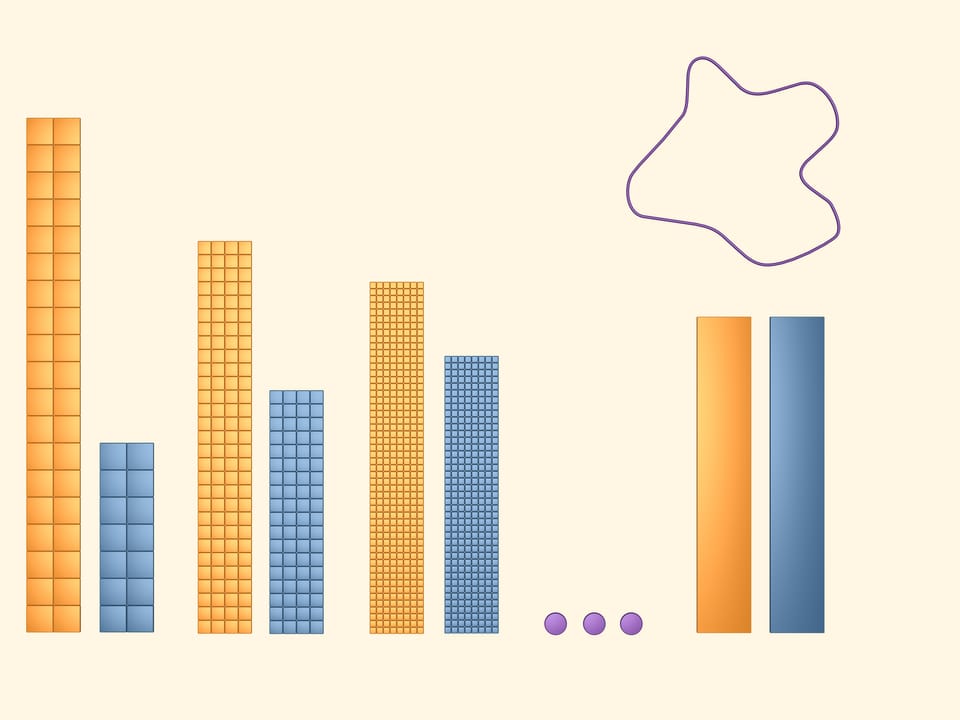
Considering an event more frequent net, we get even more precise bounds of the area of our figure.
Continue to diminish cells of the grid so that the side length of the square tends to zero. If one abstracts away from reality, one can imagine just like in mathematics that we can take arbitrary small squares. Then, as we say, in the limit the blue and the yellow rectangles composed of halves of the blue and the yellow ones (we could have considered any of them).
The area of the figure we studied is by definition the area of the two-coloured rectangle.
There are some life situations when we need an approximate area of some figure. The estimate should not differ from the value more than some given value. To do that one should take such a regular net that the difference of the areas of the yellow and the blue rectangles doesn't exceed the doubled allowed error. Then one can take the half-sum of the areas of the rectangles as the estimate.