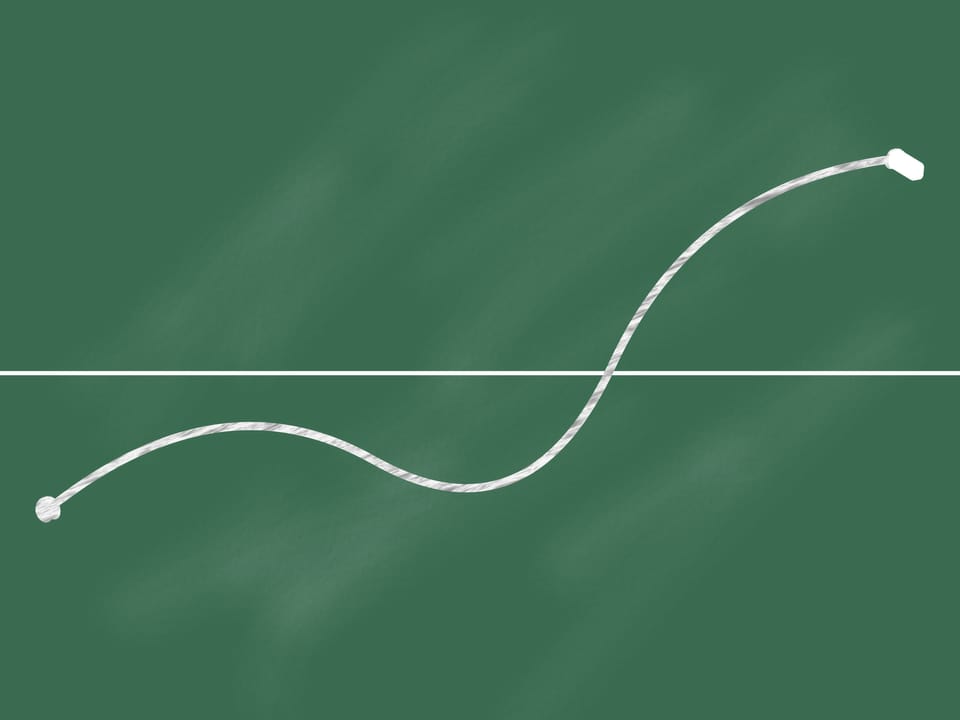
On the blackboard draw a horizontal line that divides it into two parts. Let us mark two points, one located in the lower part and one at the upper part.
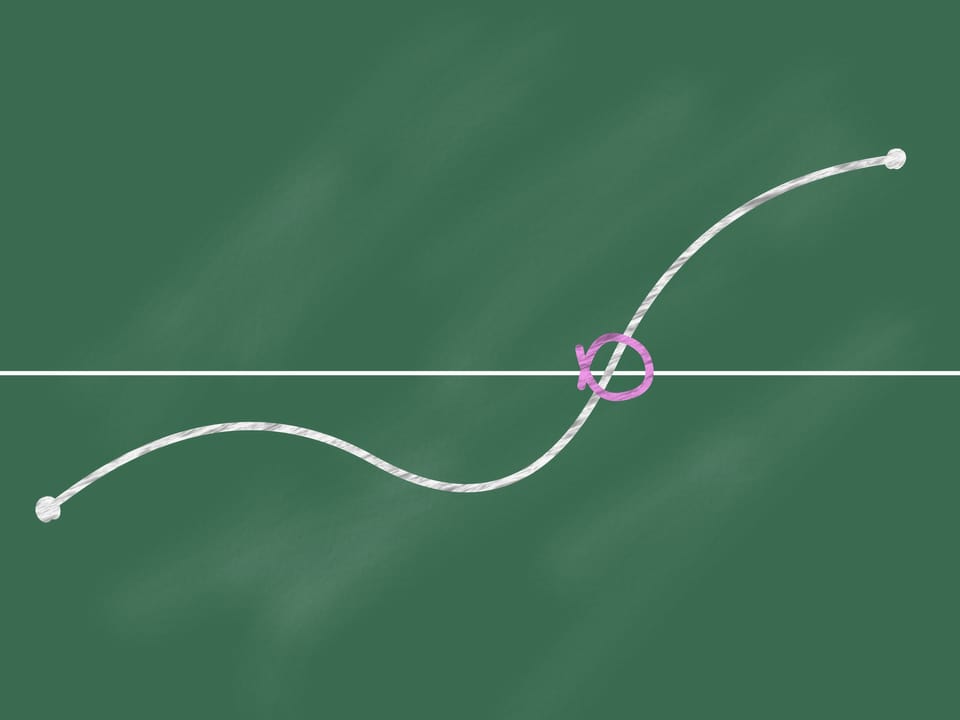
We join these points by a continuous line (i.e. not moving away the chalk from the blackboard). Then at some point (which can be not unique) our line intersects the horizontal line.
Should you think that this fact even obvious for children can be useful in mathematics? Despite the apparent obviousness, this proposition is a theorem, namely the Bolzano-Cauchy theorem, and requires a demonstration.
We will not give here the proof of this theorem, but we will observe only that all its assumptions are important, i.e. necessary. If the line is not continuous (i.e., if it were allowed to remove the chalk from the board) it is obvious that we could jump from the bottom to the top of the blackboard, without crossing the horizontal line. If we did not consider the intersection with the horizontal line (which represents the set of all real numbers), but, for example, the intersection with the set of rational numbers only, then again the intersection could be avoided.
The most surprising thing is that this seemingly childish observation is a very powerful tool used in the proof of some mathematical propositions. The drawback is that the proof is not constructive: the line somewhere cross the horizontal line, but at what point exactly, given a precise continuous line, it is impossible to say using this theorem.
Some examples of the Bolzano-Cauchy theorem will be shown in the films of Section “Continuity”.